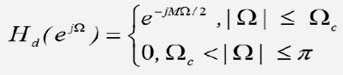Filtros IIR - Infinite Impulse Response

Na postagem anterior foi tratada a primeira classe dos filtros digitais, agora nesse material será tratada a segunda classe dos filtros digitais, filtros IIR

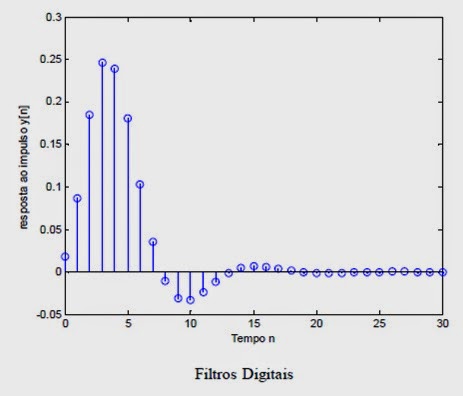
Filtros Digitais cuja resposta ao impulso apresenta duração infinita (IIR – Infinite Impulse Response)

que também pode ser reescrito como uma função racional com potências negativas de z.

No filtro IIR as características de entrada e saída são regidas por equações lineares de diferenças com coeficientes constantes de natureza recursiva, conforme pode se observar na figura a seguir.

Observa-se que no diagrama de blocos do filtro IIR, os termos , k=0,1,…,M , e os termos , j=1,…, N, são os termos da função de transferência Y(z)/X(z), normalizados pelo termo b0 .

Diagrama de Blocos

Projeto de Filtros IIR

Uma das formas de projetos de filtros digitais do tipo IIR é através da aproximação entre funções de transferências contínuas por funções de transferências discretas equivalentes. Desta forma, considera-se a seguinte aproximação em tempo discreto da função integração.

Aplicando na equação anterior o operador z, obtém-se:

implicando na seguinte aproximação:

De forma semelhante pode-se representar z em função de s, ou seja

Admitindo s=σ+jω pode-se definir regiões do Plano s e suas regiões equivalentes no Plano z.

Ou seja:

Portanto, tem-se:

 

Resultando nas seguintes propriedades para este tipo de aproximação:

1. O semiplano esquerdo do Plano s é mapeado no interior do círculo de raio unitário no Plano z;

2. O eixo jω é inteiramente mapeado sobre o circulo de raio unitário do Plano z;

3. O semiplano direito do Plano s é mapeado no exterior do círculo de raio unitário no Plano z.

Uma implicação imediata da propriedade 1 é que se o filtro analógico representado pela função de transferência Ha(s) for estável e causal, o filtro digital dele derivado através da transformação bilinear será garantidamente estável e causal.

Para σ = 0, tem-se Ω = 2 tg-1(ωT/2), concluindo-se que a faixa de frequência -∞ < ω < ∞, é comprimida em uma faixa finita de frequências contida no intervalo –π < Ω < π de um filtro digital. Esta forma de distorção não linear é conhecida como warping.

Tal distorção de fase pode ser compensada no projeto do filtro analógico através de um procedimento denominado pré-warping. Especificamente, para as frequências críticas (frequências de corte para a faixa de passagem e de rejeição), o procedimento de pré-warping é realizado de acordo com a relação:

Exemplo

Usando um filtro analógico com uma função de transferência de Butterworth de ordem 3, projetar um filtro IIR passa baixas com frequência de corte Ωc= 0.2π .

Projetos de Filtros IIR – Curva de Magnitude

Projetos de Filtros IIR – Resposta ao Impulso

Filtros FIR – Finite Impulse Response

Filtros Digitais

O processo de filtragem de sinais pode ser realizado digitalmente, na forma esquematizada pelo diagrama apresentado a seguir:

O bloco conversor A/D converte o sinal de tempo contínuo x(t) em uma sequência x[n]. O filtro digital processa a sequência x[n], resultando em outra sequência y[n], que representa o sinal filtrado na forma digital. Este sinal y[n] é então convertido para um sinal de tempo contínuo por um conversor D/A e reconstruído através de um filtro passa-baixas, cuja saída é o sinal y(t), que representará a versão filtrada do sinal x(t).

Os filtros digitais são caracterizados em duas classes, dependendo da duração da sequência y[n] quando aplicado em sua entrada um sinal do tipo impulso. Nesse material somente será tratado sobre o filtro FIR (Finite Impulse Response) e a segunda classe o filtro IIR (Infinite Impulse Response) será tratado em outro material.

Filtros Digitais cuja resposta ao impulso apresenta duração finita (FIR – Finite Impulse Response)

Estes filtros apresentam a seguinte função de transferência discreta:

 que pode ser reescrito como uma função polinomial com potências negativas de z.

Características

-> Memória finita, portanto qualquer transitório tem duração limitada;

-> São sempre BIBO^* estáveis;

-> Podem implementar uma resposta em módulo desejada com resposta em fase linear.

* O sistema será BIBO estável (Bounded Input Bounded Output) se para todo sinal de entrada limitado implicar em um sinal de saída limitado.

 Diagrama de Blocos Filtro FIR

Projeto de Filtros FIR

Uma vez que os filtros FIR apresentam resposta em frequência com fase linear, o projeto deste filtros resume-se a aproximar a resposta em módulo desejada.

Admitindo h[n] como sendo a resposta ao impulso de um filtro FIR, sendo H(ejΩ) a transformada discreta de Fourier de h[n]. Uma vez definida a ordem do filtro, por exemplo M, deve-se então determinar os ak , k=0,1,…,M, coeficientes do filtro.

O objetivo na determinação dos coeficientes é que H(ejΩ) forneça uma boa aproximação de Hd(ejΩ), que é a função resposta em frequência desejada ao longo do intervalo de frequências –π < Ω ≤ π. Uma forma de avaliar a qualidade desta aproximação é através do erro médio quadrático entre hd[n] e h[n], ou seja:

                                                

Os únicos parâmetros ajustáveis na equação anterior são os coeficientes do filtro H(ejΩ), ak , k=0,1,…,M, sendo a medida do erro minimizada fazendo

 A relação apresentada anteriormente equivale ao uso de uma janela retangular definida por

 Portanto 

             

que conhecido como o método da janela.

A convolução de W(ejΩ) com Hd(ejΩ) resulta em uma aproximação oscilatória da função resposta em frequência desejada por H(ejΩ) do filtro FIR. Tais oscilações podem ser reduzidas modificando-se a janela a ser utilizada.

Resposta em frequência da janela retangular.

Uma janela comumente utilizada é a janela de Hamming, definida por

Característica da janela de Hamming

Resposta de frequência das duas janelas

Pelo apresentado nas curvas de resposta em frequência das duas janelas conclui-se:

* O lóbulo principal da janela retangular tem aproximadamente a metade da largura do lóbulo principal da janela de Hamming;

* A magnitude dos lóbulos laterais da janela de Hamming são bem mais reduzidos se comparados com o da janela retangular.

Segue abaixo exemplo para comparação entre as duas janelas :

Exemplo:

Considere a resposta em frequência desejada

que representa a função resposta em frequência de um filtro passa baixas ideal, com fase linear. Avaliar a resposta em frequência para M=12, Ωc=0.2π, sendo:

(a) janela retangular

(b) janela de Hamming.

 Solução:

 Coeficientes normalizados para | H(z) |z=1 = 1

Transformada Z

Introdução

 A Transformada de Fourier de Tempo Discreto (TFTD) desempenha um papel relevante na representação e análise de sinais e sistemas discretos. A Transformada Z é uma generalização da TFTD.

A TZ está para os sinais discretos assim como a Transformada de Laplace está para os sinais analógicos e ambas estão relacionadas com a TF correspondente.

A TFTD não existe para todas as sequências e é importante ter uma generalização que engloba uma classe mais ampla de sinais.

A TZ proporciona a utilização da teoria de variáveis complexas em questões de Processamento Digital de Sinais.

Definição - A Transformada Z da seqüência x[n] é:

onde Z é uma variável complexa.

Note que a TFTD pode ser obtida da TZ simplesmente fazendo-se:

ou seja , 

                

Esta é a razão para a notação X(e^jw) para a TFTD.

Assim, quando a TFTD existe, ela é obtida de X(Z) fazendo-se Z = e^jw.

Portanto, quando |Z| = 1, a TZ corresponde a TFTD.

Notação :

Região de Convergência

Sendo a TZ uma função de variável complexa, é conveniente representá-la no plano Z complexo.

Neste, plano, a região |Z| = 1 corresponde ao círculo de raio unitário.

Os valores de Z para os quais a TZ existe (ou a série converge) definem uma região chamada Região de Convergência (ROC).

Pólos e Zeros

A TZ é muito útil quando a série infinita tem uma forma fechada do tipo

 onde P(Z) e Q(Z) são polinômios em Z.

As raízes de P(Z) e Q(Z) são chamadas, respectivamente, de ZEROS e PÓLOS de X(Z) .

Propriedades da Região de Convergência

A região de convergência (ROC) traz algumas propriedades:

1) A ROC é um anel ou disco no Plano Z com centro na origem.

2) A TF da seqüência x[n] converge absolutamente se e somente se a ROC da TZ contém o círculo unitário.

3) A ROC não pode conter pólos.

4) Se x[n] é uma seqüência de duração finita, a ROC é todo plano Z.

5) Se x[n] é causal (right-sided), a ROC estende-se para além dos pólos mais externos, possivelmente tendendo a infinito.

6) Se x[n] é não causal (left-sided), a ROC extende-se para uma região menor que o menor pólo até zero.

7) Se x[n] é uma seqüência com componentes parte causal e parte não-causal, então a ROC é um anel.

8) A ROC é uma região conectada.

Propriedades da Transformada Z

Notação:

T1. Linearidade

T2. Deslocamento no Tempo

T3. Multiplicação por uma Seqüência Exponencial

T4. Diferenciação na Freqüência

                          

T5. Inversão no Tempo

 T6. Convolução

T7. Valor Inicial

Se x[n] é causal

As Tz mais importantes são as dadas por uma função racional dentro da ROC, uma vez que seus coeficientes são usados na construção de filtros.

X(z) = P(z) -> zeros de x(z) => raízes de P(z)

           Q(z) ->pólos de x(z) => raízes de Q(z)

Lab - Transformada de Fourier Discreta

Processamento Digital de sinais

Prof. Débora Meyhofer Ferreira 

Transformada de Fourier Discreta

MatLab

Laboratório

1) Digitar o programa a seguir para determinar a a magnitude e fase, assim como a parte real e imaginária de x(n) = (0,5)ⁿ u(n), usando 501 pontos espaçados entre [0, π].

Como:

No Matlab:

w = [0:1:500]*pi/500;   %eixo dividido em 501 pontos

x = exp(j*w) ./ (exp(j*w) - 0.5*ones(1,501));

magx = abs(x);angx = angle(x);

realx = real(x); imagx = imag(x);

subplot(2,2,1); plot(w/pi,magx); grid

xlabel('frenquencia em PI unidades'); title('Parte de Magnetude'); ylabel('Magnetude')

subplot(2,2,3); plot(w/pi,angx); grid

xlabel('frenquencia em PI unidades'); title('Parte do Angulo'); ylabel('Radiano')

subplot(2,2,2); plot(w/pi,realx); grid

xlabel('frenquencia em PI unidades'); title('Parte Real'); ylabel('Real')

subplot(2,2,4); plot(w/pi,imagx); grid

xlabel('frenquencia em PI unidades'); title('Parte Imaginaria'); ylabel('Imaginario')

2). De maneira similar ao exemplo 1, escreva um programa no MatLab que plote |X(e^jw)| e ∠ X(e^jw) da sequência abaixo, usando 501 freqüências equidistantes no intervalo [0,π].

x(n)={1,2,3,4,5}

No Matlab:

n = -1:3; x = 1:5;

k = 0:500; w = (pi/500)*k;

x = x * (exp(-j*pi/500)) .^ (n'*k);

w = [0:1:500]*pi/500;   %eixo dividido em 501 pontos

magx = abs(x);angx = angle(x);

realx = real(x); imagx = imag(x);

subplot(2,2,1); plot(w/pi,magx); grid

xlabel('frenquencia em PI unidades'); title('Parte de Magnetude'); ylabel('Magnetude')

subplot(2,2,3); plot(w/pi,angx); grid

xlabel('frenquencia em PI unidades'); title('Parte do Angulo'); ylabel('Radiano')

subplot(2,2,2); plot(w/pi,realx); grid

xlabel('frenquencia em PI unidades'); title('Parte Real'); ylabel('Real')

subplot(2,2,4); plot(w/pi,imagx); grid

xlabel('frenquencia em PI unidades'); title('Parte Imaginaria'); ylabel('Imaginario')

3) Encontre a resposta em freqüência H(e ^jw ) de h(n) = 0,9ⁿ u(n) (feito em classe). Plote a amplitude e fase.

No Matlab:

w = [0:1:500]*pi/500;   %[0, pi] eixo dividido em 501 pontos

H = exp(j*w) ./ (exp(j*w) - 0.9*ones(1,501));

magH = abs(H);angH = angle(H);

realH = real(H); imagH = imag(H);

subplot(2,2,1); plot(w/pi,magH); grid

xlabel('frenquencia em PI unidades'); title('Parte de Magnetude'); ylabel('Magnetude')

subplot(2,2,3); plot(w/pi,angH); grid

xlabel('frenquencia em PI unidades'); title('Parte do Angulo'); ylabel('Radiano')

subplot(2,2,2); plot(w/pi,realH); grid

xlabel('frenquencia em PI unidades'); title('Parte Real'); ylabel('Real')

subplot(2,2,4); plot(w/pi,imagH); grid

xlabel('frenquencia em PI unidades'); title('Parte Imaginaria'); ylabel('Imaginario')

4) Um filtro passa-baixa de 3. ordem é descrito pela seguinte equação de diferenças:

Plote a resposta em freqüência do filtro para confirmar o seu comportamento.

No Matlab:

b = [0.0181, 0.0543, 0.0543, 0.0181];   %Coeficiente de filtro matriz b

a = [1.0000, -1.7600, 1.1829, -0.2781]; %Coeficiente de filtro matriz a

m = 0:length(b)-1; l = 0:length(a)-1;   %Indice das matrizes m e l

K = 500; k = 0:1:K;                     %Indice da matriz k para frequencias

w = pi*k/K;                             %[0, pi] eixo divido em 501 pontos

num = b * exp(-j*m'*w);                 %Calculos do numerador

den = a * exp(-j*l'*w);                 %Calculos do denominador

H = num ./ den;                         %Resposta à frequencia

magH = abs(H); angH = angle(H);         %Resposta à fase e magnetude

subplot(1,1,1);

subplot(2,1,1); plot(w/pi,magH); grid; axis([0,1,0,1])

xlabel('frenquencia em PI unidades'); ylabel('|H|');

title('resposta Magnetude');

subplot(2,1,2); plot(w/pi,angH/pi); grid

xlabel('frenquencia em PI unidades'); ylabel('Fase em PI Radianos')

title('resposta Fase');