Filtros Digitais
O processo de
filtragem de sinais pode ser realizado digitalmente, na forma esquematizada
pelo diagrama apresentado a seguir:

O bloco conversor A/D
converte o sinal de tempo contínuo x(t) em uma sequência x[n]. O filtro digital
processa a sequência x[n], resultando em outra sequência y[n], que representa o
sinal filtrado na forma digital. Este sinal y[n] é então convertido para um
sinal de tempo contínuo por um conversor D/A e reconstruído através de um
filtro passa-baixas, cuja saída é o sinal y(t), que representará a versão
filtrada do sinal x(t).
Os filtros digitais
são caracterizados em duas classes, dependendo da duração da sequência y[n]
quando aplicado em sua entrada um sinal do tipo impulso. Nesse material somente
será tratado sobre o filtro FIR (Finite Impulse Response) e a segunda classe o
filtro IIR (Infinite Impulse Response) será tratado em outro material.
Filtros Digitais cuja
resposta ao impulso apresenta duração finita (FIR – Finite Impulse Response)
Estes filtros apresentam
a seguinte função de transferência discreta:

Características
-> Memória finita,
portanto qualquer transitório tem duração limitada;
-> São sempre BIBO*
estáveis;
-> Podem
implementar uma resposta em módulo desejada com resposta em fase linear.
* O sistema será BIBO estável (Bounded Input
Bounded Output) se para todo sinal de entrada limitado implicar em um sinal de
saída limitado.
Projeto de Filtros FIR
Uma vez que os filtros FIR apresentam resposta em frequência com fase
linear, o projeto deste filtros resume-se a aproximar a resposta em módulo desejada.
Admitindo h[n] como sendo a resposta ao impulso de um filtro FIR, sendo
H(ejΩ) a transformada discreta de Fourier de h[n]. Uma vez definida a ordem do
filtro, por exemplo M, deve-se então determinar os ak , k=0,1,…,M, coeficientes
do filtro.
O objetivo na determinação dos coeficientes é que H(ejΩ) forneça uma boa
aproximação de Hd(ejΩ), que é a função resposta em frequência desejada ao longo
do intervalo de frequências –π < Ω ≤ π. Uma forma de avaliar a qualidade
desta aproximação é através do erro médio quadrático entre hd[n] e h[n], ou
seja:
Os únicos parâmetros ajustáveis na equação anterior são os coeficientes
do filtro H(ejΩ), ak , k=0,1,…,M, sendo a medida do erro minimizada fazendo
que conhecido como o método da janela.
A convolução de W(ejΩ)
com Hd(ejΩ) resulta em uma aproximação oscilatória da função resposta em frequência
desejada por H(ejΩ) do filtro FIR. Tais oscilações podem ser reduzidas modificando-se
a janela a ser utilizada.
Resposta em frequência da janela retangular.
Uma janela comumente
utilizada é a janela de Hamming, definida por
Característica da janela de
Hamming
Resposta de frequência das duas
janelas
Pelo apresentado nas curvas de resposta em frequência das duas janelas
conclui-se:
* O lóbulo principal da janela retangular tem aproximadamente a metade
da largura do lóbulo principal da janela de Hamming;
* A magnitude dos lóbulos laterais da janela de Hamming são bem mais
reduzidos se comparados com o da janela retangular.
Segue abaixo exemplo para comparação entre as duas janelas :
Exemplo:
Considere a resposta em frequência desejada
que representa a função resposta em frequência de um filtro passa baixas
ideal, com fase linear. Avaliar a resposta em frequência para M=12, Ωc=0.2π,
sendo:
(a) janela retangular
(b) janela de Hamming.
Solução:
Coeficientes normalizados para |
H(z) |z=1 = 1











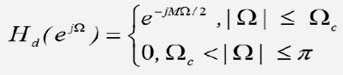


Nenhum comentário:
Postar um comentário